JEE 2014 :: Advanced 2014 :: Physics 2014

• Advanced 2014 - Physics 2014
• Advanced 2014 - Chemistry 2014
• Advanced 2014 - Mathematics 2014

 Two parallel wires in the plane of the paper are distance X₀ apart. A point charge is moving with speed u between and wires in the same plane at a distance X₁ from one of the wires. When the wires carry current of magnitude I in the same direction, the radius of curvature of the path of the point charge is R₁. In contrast, if the currents in the two wires have directions opposite to each other, the radius of curvature of the path is R₂. If   $\frac{X_{0}}{X_{1}}=3$ , and value of R₁/R₂ is

Answer:

Explanation:

$B_{2}=\frac{\mu_{0}I}{2\pi x_{1}}+\frac{\mu_{0}I}{2\pi(x_{0}-x_{1})}$

        { when  currents are in opposite directions)

$B_{1}=\frac{\mu_{0}I}{2\pi x_{1}}-\frac{\mu_{0}I}{2\pi(x_{0}-x_{1})}$

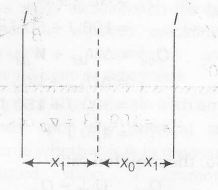
(when currents are in same direction)

Subtituting $x_{1}=\frac{x_{0}}{3}$ as \left(\frac{x_{0}}{x_{1}}\right)

$B_{1}=\frac{3\mu_{0}I}{2\pi x_{0}}-\frac{3\mu_{0}I}{4\pi x_{0}}=\frac{3\mu_{0}I}{4\pi x_{0}}$

    $R_{1}=\frac{mv}{qB_{1}} $   and  $ B_{2}= \frac{9\mu_{0}I}{4\pi x_{0}}$

 $R_{2}=\frac{mv}{qB_{2}} $

$\frac{R_{1}}{R_{2}}=\frac{B_{2}}{B_{1}}=\frac{9}{3}=3$

 A uniform circular disc of mass 1.5 kg and radius 0.5m  is initially at rest on a  horizontal frictionless surface. Three forces of equal magnitude  F=0.5N  are applied simultaneously along the three sides of an equilateral triangle XYZ with its vertices on the perimeter of the disc (see figure) . One second after applying the forces, the angular speed of the disc in rad s^-1 is 

Answer:

Explanation:

  Angular impluse = change in angular momentum

  $\therefore$      $\int_{}^{} \tau dt=I\omega$

    $\Rightarrow$    $ \omega=\frac{\int_{}^{}\tau dt }{I}$

$=\frac{\int_{}^{}3F \sin 30^{0}R dt }{I}$

 substituting the values, we have

$\omega=\frac{3(0.5)(0.5)(0.5)(1)}{\frac{1.5(0.5)^{2}}{2}}=2rad/s$

During Searle's experiment, zero of the vernier scale lies between $3.20\times 10^{-2}$ m and $3.25\times 10^{-2}$ m of the main scale. The 20th division of the vernier scale exactly coincides with one of the main scale divisions. When an additional load of 2 kg is applied to the wire, the zero of the vernier scale still lies between  $3.20\times 10^{-2}$ m and $3.25\times 10^{-2}$ m²   of the main scale but now the 45th division of the vernier scale coincides with one of the main scale divisions. The length of the thin metallic wire is 2m and its cross-sectional area is  $8\times 10^{-7}$ m. The least count of the vernier scale is  $1.0\times 10^{-5}$ m. The maximum percentage  error in the YOung's modulus of the wire is

Answer:

Explanation:

$Y=\frac{F/A}{\frac{\triangle l}{l}}, \triangle l=25\times 10^{-50}m$

   $Y=\frac{F}{A}.\frac{l}{\triangle l}$

$\frac{\triangle Y}{Y}\times 100=\frac{10^{-5}}{25\times 10^{-5}}\times100=4$  %

Aeroplanes A and B are flying with constant velocity in the same vertical plane at angles 30°  and 60° with respect to the horizontal respectively as shown in the figure. The speed of A is   $100\sqrt{3}$ ms^-1. At time t=0 s, an observer in A Finds B at a distance of 500m. This observer sees B moving with a constant velocity perpendicular to the line of motion of A. If at t=t₀, A just escapes being hit by B, t₀ in seconds is 

Answer:

Explanation:

 The relative velocity of B with respect to A is perpendicular to line PA. Therefore, along line PA, velocity components of A and B should be the same.

$\Rightarrow $    $V_{A}=100\sqrt{3}=V_{B}\cos 30^{0}$

$\Rightarrow$   V_B=200m/s

$t_{0}=\frac{500}{V_{B}\sin 30^{0}}$

  $=\frac{500}{200\times\frac{1}{2}}=5s$

 Two ideal batteries of emf V₁  and V₂    and three resistance R₁, R₂  and R₃ are connected as shown in the figure. The current in resistance  R₂ would be zero if

Answer:

Explanation:

Let us take  $V_{P}=0$  .Then potentials  acrosds  $R_{1}$, $R_{2}$   and $R_{3}$ are as shown in figure(ii)

In the same figure.

      i₁ +i₂  =i₃

$\therefore$    $ \frac{V_{1}-V_{0}}{R_{1}}+\frac{0-V_{0}}{R_{2}}=\frac{V_{0}-(-V_{2})}{R_{3}}$

 Solving this equation  we get,

 $V_{0}=\frac{\frac{V_{1}}{R_{1}}+0-\frac{V_{2}}{R_{2}}}{\frac{1}{R_{1}}+\frac{1}{R_{2}}+\frac{1}{R_{3}}}$

  Current througfh R₂ will be zero if

$V_{0}=0\Rightarrow\frac{V_{1}}{V_{2}}=\frac{R_{1}}{R_{2}}$

 In options (a),(b), and (d)  this reaction is satisfied

• Advanced 2014 - Physics 2014
• Advanced 2014 - Chemistry 2014
• Advanced 2014 - Mathematics 2014